Identifying Cloud Types
Earlier this week you may have seen pictures of a rare cloud formation when the people of Wonthaggi, in Victoria, shared pictures of a rare, rainbow-filled "hole punch" cloud on Monday. These are also called a fallstreak cloud and are formed after an airplane flies through a cooler, cloudy region and leaves behind a trail of ice crystals.
With a water cloud at a mid-level of about 10,000 feet, the plane flying overhead will leave a condensation trail that produces ice crystals. When the right conditions mix, the ice crystals will grow as they gather moisture from surrounding water droplets.
Very Pretty!
This reminded us that we've been collecting photographs of different clouds you see over Pittwater to share with you and this rare cloud being seen makes this a timely insight for all those who love seeing fluffy rabbits and elephant shapes in clouds to also have a look at what kinds of clouds these really are.
In meteorology, a cloud is a visible mass of liquid droplets or frozen crystals made of water or various chemicals suspended in the atmosphere above the surface of a planetary body. Clouds in earth's atmosphere are studied in the cloud physics branch of meteorology. Terrestrial cloud formation is the result of air in Earth's atmosphere becoming saturated due to either or both of two processes: cooling of the air and adding water vapor.
Clouds in the troposphere, the atmospheric layer closest to Earth's surface, have Latin names due to the universal adaptation of Luke Howard's nomenclature. Luke Howard was a British manufacturing chemist and an amateur meteorologist. His contribution to science is a nomenclature system for clouds, which he proposed in an 1802 presentation to the Askesian Society. It was introduced in December 1802 and became the basis of a modern international system that classifies these tropospheric aerosols into several physical forms, then cross-classifies them as low-, middle- and high-étage according to cloud-base altitude range above Earth's surface.
Nomenclature is a system of names or terms, or the rules for forming these terms in a particular field of arts or sciences. The scientific need for simple, stable and internationally accepted systems for naming objects of the natural world has generated many formal nomenclatural systems. Probably the best known of these nomenclatural systems are the five codes of biological nomenclature that govern the Latinized scientific names of organisms.
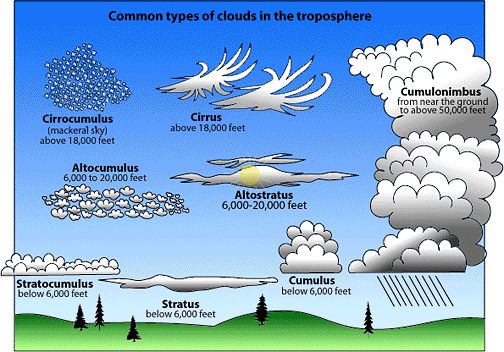Clouds are commonly grouped into physical forms that can be up to five in number: cirriform, cumuliform, cumulonimbiform, stratocumuliform, and stratiform. These designations distinguish a cloud's physical structure and process of formation.
Clouds are formed as all air contains water, but near the ground it is usually in the form of an invisible gas called water vapor. When warm air rises, it expands and cools. Cool air can't hold as much water vapor as warm air, so some of the vapor condenses onto tiny pieces of dust that are floating in the air and forms a tiny droplet around each dust particle. When billions of these droplets come together they become a visible cloud.
When clouds form they appear white to us because their water droplets or ice crystals are large enough to scatter the light of the seven colour wavelengths (red, orange, yellow, green, blue, indigo, and violet), which combine to produce white light.
Clouds turn gray if the clouds get thick enough or high enough and all the light above does not make it through , making a cloud appear gray or dark look. If there are lots of other clouds around, their shadow can add to the gray or multicolored gray appearance.
Clouds move with the wind. High cirrus clouds are pushed along by the jet stream, sometimes traveling at more than 100 miles-per-hour. When clouds are part of a thunderstorm they usually travel at 30 to 40 mph.
Fog is also a Cloud form! There are many different types of fog, but fog is mostly formed when warm winds moist air into a region. As the warm, moist air flows over much colder soil dense fog often forms. Warm, moist air is cooled from below as it flows over a colder surface. If the air is near saturation, moisture will condense out of the cooled air and form fog. With light winds, the fog near the ground can become thick and reduce visibilities to zero.
Cloud Types
Cirrus Clouds are the most common of the high clouds. They are composed of ice and are thin, wispy clouds blown in high winds into long streamers. Cirrus clouds are usually white and predict fair to pleasant weather. By watching the movement of cirrus clouds you can tell from which direction weather is approaching. When you see cirrus clouds, it usually means that a change in the weather will occur within 24 hours.
Cirrus Clouds over Pittwater
Cirrostratus clouds are thin, sheetlike high clouds that often cover the entire sky. They are so thin that the sun and moon can be seen through them. Cirrostratus clouds usually come 12-24 hours before a rain storm.
Cirrostratus clouds over Avalon Beach
Cirrocumulus clouds appear as small, rounded white puffs that appear in long rows. The small ripples in the cirrocumulus clouds sometime resemble the scales of a fish. Cirrocumulus clouds are usually seen in the winter and indicate fair, but cold weather. In tropical regions, they may indicate an approaching hurricane!
Cirrocumulus clouds over Careel Bay playing fields - and more of them over Mona Vale Village Park
Altostratus clouds are gray or blue-gray mid level clouds composed of ice crystals and water droplets. The clouds usually cover the entire sky. In the thinner areas of the clouds, the sun may be dimly visible as a round disk. Altostratus clouds often form ahead of storms with continuous rain.
Altocumulus clouds are mid level clouds that are made of water droplets and appear as gray puffy masses. They usually form in groups. If you see altocumulus clouds on a warm, sticky morning, be prepared to see thunderstorms late in the afternoon.
Stratus clouds are uniform grayish clouds that often cover the entire sky. They resemble fog that doesn't reach the ground. Light mist or drizzle sometimes falls out of these clouds.
Stratocumulus clouds are low, puffy and gray. Most form in rows with blue sky visible in between them. Rain rarely occurs with stratocumulus clouds, however, they can turn into nimbostratus clouds.
Nimbostratus clouds form a dark gray, wet looking cloudy layer associated with continuously falling rain or snow. They often produce precipitation that is usually light to moderate.
Cumulus clouds are white, puffy clouds that look like pieces of floating cotton. Cumulus clouds are often called "fair-weather clouds". The base of each cloud is flat and the top of each cloud has rounded towers. When the top of the cumulus clouds resemble the head of a cauliflower, it is called cumulus congestus or towering cumulus. These clouds grow upward and they can develop into giant cumulonimbus clouds, which are thunderstorm clouds.
Cumulus Cloud
Cumulonimbus clouds are thunderstorm clouds. High winds can flatten the top of the cloud into an anvil-like shape. Cumulonimbus clouds are associated with heavy rain, snow, hail, lightning and even tornadoes. The anvil, if there is one, usually points in the direction the storm is moving.
Cumulonimbus cloud
Mammatus clouds are low hanging bulges that droop from cumulonimbus clouds. Mammatus clouds are usually associated with severe weather.
Lenticular clouds are caused by a wave wind pattern created by the mountains. They look like discs or flying saucers that form near mountains.
Fog is a cloud on the ground. It is composed of billions of tiny water droplets floating in the air. Fog exists if the atmospheric visibility near the Earth's surface is reduced to 1 kilometer or less.
Contrails are condensation trails left behind jet aircrafts. Contrails form when hot humid air from jet exhaust mixes with environmental air of low vapor pressure and low temperature. The mixing is a result of turbulence generated by the engine exhaust.
Fractus clouds are small, ragged cloud fragments that are usually found under an ambient cloud base. They form or have broken off from a larger cloud, and are generally sheared by strong winds, giving them a jagged, shredded appearance. Fractus have irregular patterns, appearing much like torn pieces of cotton candy. They change constantly, often forming and dissipating rapidly. They do not have clearly defined bases. Sometimes they are persistent and form very near the surface.
Green Clouds are often associated with severe weather. The green color is not completely understood, but it is thought to have something to do with having a high amount of liquid water drops and hail inside the clouds.
References:
1. Sydney region. NSW Government 3.1. Page updated 23rd of March, 2012. Retrieved from http://www.environment.nsw.gov.au/air/nepm/301sydney.htm
2. Cloud. (2013, February 6). In Wikipedia, The Free Encyclopedia. Retrieved from http://en.wikipedia.org/w/index.php?title=Cloud&oldid=536920975